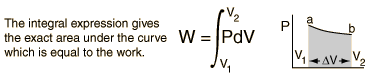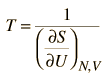How to Measure Heat Flow &
Enthalpy Change
A calorimeter is a device that is used to measure the
quantity of heat flow in a chemical reaction. Two common types of
calorimeters are the coffee cup calorimeter and the bomb
calorimeter.
Coffee Cup Calorimeter
A coffee cup calorimeter is essentially a polystyrene
(Styrofoam) cup with a lid. Really, any well-insulated container
will work. The cup is partially filled with a known volume of
water and a thermometer is inserted through the lid of the cup so
that the thermometer bulb is below the water surface. The water
absorbs the heat of any chemical reaction taking place in the
calorimeter. The change in the water temperature is used to
calculate the amount of heat that has been absorbed (used to make
products, so water temperature decreases) or evolved (lost to the
water, so its temperature increases) in the reaction.
Heat flow is calculated using the relation:
q =
Cp . m . Dt
where
q
is heat flow, m is mass in grams, and Dt is the change in temperature
in °C. The
specific heat
Cpis the amount of heat required to raise the
temperature of 1 gram of a substance 1 degree Celsius.
The
specific heat of (pure) water is 4.186 J/(g·°C).
For example, consider a chemical reaction which occurs in 200
grams of water with an initial temperature of 25.0°C. The reaction
is allowed to proceed in the coffee cup calorimeter. As a result
of the reaction, the temperature of the water changes to 31.0°C.
The heat flow is calculated:
qwater = 4.186 J/(g·°C)
. 200 g . (31.0°C - 25.0°C)
qwater = +5.0 x 103 J
In other words, the products of the reaction evolved 5000 J of
heat, which was lost to the water. The enthalpy change,
DH, for the reaction is equal in
magnitude but opposite in sign to the heat flow for the water:
DHreaction = -(qwater)
For an exothermic reaction, DH
< 0; qwater is positive. The water absorbs heat from
the reaction and an increase in temperature is seen. For an
endothermic reaction, DH
> 0; qwater
is negative. The water supplies heat for the reaction and a
decrease in temperature is seen.
Bomb Calorimeter
A coffee cup calorimeter is great for measuring heat flow in a
solution, but it can't be used for reactions which involve gases,
since they would escape from the cup. Also, a coffee cup
calorimeter can't be used for high temperature reactions, since
high heat would melt the cup. A bomb calorimeter is used to
measure heat flows for gases and high temperature reactions.
A bomb calorimeter works the same way as a coffee cup
calorimeter, with one big difference. In a coffee cup calorimeter,
the reaction takes place in the water. In a bomb calorimeter, the
reaction takes place in a sealed metal container, which is placed
in the water in an insulated container. Heat flow from the
reaction crosses the walls of the sealed container to the water.
The temperature difference of the water is measured, just as it
was for a coffee cup calorimeter. Analysis of the heat flow is a
bit more complex than it was for the coffee cup calorimeter
because the heat flow into the metal parts of the calorimeter must
be taken into account:
qreaction = - (qwater + qbomb)
where qwater = 4.18 J/(g·°C)
. mwater .
Dt
The bomb has a fixed mass and specific heat. The mass of the
bomb multiplied by its specific heat is sometimes termed the
calorimeter constant, denoted by the symbol C with units of
joules per degree Celsius. The calorimeter constant is determined
experimentally and will vary from one calorimeter to the next. The
heat flow of the bomb is:
qbomb = C . Dt
Once the calorimeter constant is known, calculating heat flow
is a simple matter. The pressure within a bomb calorimeter often
changes during a reaction, so the heat flow may not be equal in
magnitude to the enthalpy change.
|
First Law of Thermodynamics
The first law of thermodynamics is the application of the
conservation of energy principle to heat and thermodynamic processes:
The first law makes use of the key concepts of internal energy, heat,
and system work. It is used extensively in the discussion of heat
engines.
It is typical for chemistry texts to write the first law as ΔU=Q+W.
It is the same law, of course - the thermodynamic expression of the
conservation of energy principle. It is just that W is defined as the
work done on the system instead of work done by the
system. In the context of physics, the common scenario is one of adding
heat to a volume of gas and using the expansion of that gas to do work,
as in the pushing down of a piston in an internal combustion engine. In
the context of chemical reactions and process, it may be more common to
deal with situations where work is done on the system rather than by it.
Enthalpy
Four quantities called "thermodynamic potentials" are useful in the
chemical thermodynamics of reactions and non-cyclic processes. They are
internal energy, the enthalpy, the Helmholtz free energy and the Gibbs
free energy. Enthalpy is defined by
H = U + PV
where P and V are the pressure and volume, and U is internal energy.
Enthalpy is then a precisely measurable state variable, since it is
defined in terms of three other precisely definable state variables. It
is somewhat parallel to the first law of thermodynamics for a constant
pressure system
Q = ΔU + PΔV since in this case Q=ΔH
It is a useful quantity for tracking chemical reactions. If as a result
of an exothermic reaction some energy is released to a system, it has to
show up in some measurable form in terms of the state variables. An
increase in the enthalpy H = U + PV might be associated with an increase
in internal energy which could be measured by calorimetric, or with work
done by the system, or a combination of the two.
The internal energy U might be thought of as the energy required to
create a system in the absence of changes in temperature or volume. But
if the process changes the volume, as in a chemical reaction which
produces a gaseous product, then work must be done to produce the change
in volume. For a constant pressure process the work you must do to
produce a volume change ΔV is PΔV. Then the term PV can be interpreted
as the work you must do to "create room" for the system if you presume
it started at zero volume.
System Work
When work is done by a thermodynamic system, it is usually a gas that
is doing the work. The work done by a gas at constant pressure is:
For non-constant pressure, the work can be visualized as the area
under the pressure-volume curve which represents the process taking
place. The more general expression for work done is:
Work
done by a system decreases the internal energy of the system, as
indicated in the First Law of Thermodynamics. System work is a major
focus in the discussion of heat engines.
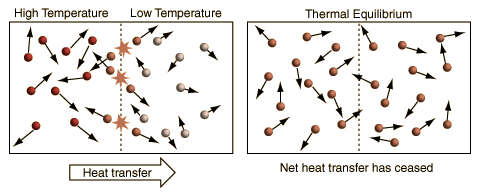
A More General View of
Temperature
When a high temperature object is placed in contact with a low
temperature object, then energy will flow from the high temperature
object to the lower temperature object, and they will approach an
equilibrium temperature. When the details of this common-sense scenario
are examined, it becomes evident that the simple view of temperature
embodied in the commonly used kinetic temperature approach has some
significant problems.
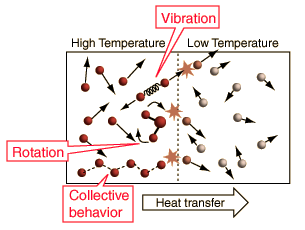
The above illustration summarizes the situation when the kinetic
temperature gives a reasonable general description of the nature of
temperature. For monoatomic gases acting like point masses, a higher
temperature simply implies higher average kinetic energy. Faster
molecules striking slower ones at the boundary in elastic collisions
will increase the velocity of the slower ones and decrease the velocity
of the faster ones, transferring energy from the higher temperature to
the lower temperature region. With time, the molecules in the two
regions approach the same average kinetic energy (same temperature) and
in this condition of thermal equilibrium there is no longer any net
transfer of energy from one object to the other.
|
 |
The concept of
temperature is complicated by internal degrees of freedom like
molecular rotation and vibration and by the existence of internal
interactions in solid materials which can include collective modes.
The internal motions of molecules affect the specific heats of
gases, with diatomic hydrogen being the classic case. Collective
modes affect the specific heats of solids, particularly at low
temperatures. |
Complications such as these have led to the adoption of a different
approach to the concept of temperature in the study of thermodynamics.
Schroeder's proposal for a theoretical definition of temperature is:
- "Temperature is a measure of the tendency of an
object to spontaneously give up energy to its surroundings. When two
objects are in thermal contact, the one that tends to spontaneously
lose energy is at the higher temperature, one loses and another one
gains."
The kinetic temperature for monoatomic ideal gases described above is
consistent with this definition of temperature for the simple systems to
which it applies. In that case the equilibrium reached is one of maximum
entropy, and the rate of approach to that state will be proportional to
the difference in temperature between the two parts of the system.
Noting that the equilibrium state of a collection of particles will be
the state of greatest multiplicity, then one can define the temperature
in terms of that multiplicity (entropy) as follows:
Temperature is expressed as the inverse of the rate of change of entropy
with internal energy, with volume V and number of particles N held
constant. This is certainly not as intuitive as molecular kinetic
energy, but in thermodynamic applications it is more reliable and more
general.
Specific Heat
Capacities Table
|
Substance |
J/g/oC
or J/g/K |
cal/g/oC
or cal/g/K |
|
Water (0 oC to 100 oC) |
4.186 |
1.000 |
|
Methyl Alcohol |
2.549 |
0.609 |
|
Ice (-10 oC to 0 oC) |
2.093 |
0.500 |
|
Steam (100 oC) |
2.009 |
0.480 |
|
Benzene |
1.750 |
0.418 |
|
Wood (typical) |
1.674 |
0.400 |
|
Soil (typical) |
1.046 |
0.250 |
|
Air (50 oC) |
1.046 |
0.250 |
|
Aluminum |
0.900 |
0.215 |
|
Marble |
0.858 |
0.205 |
|
Glass (typical) |
0.837 |
0.200 |
|
Iron/Steel |
0.452 |
0.108 |
|
Copper |
0.387 |
0.0924 |
|
Silver |
0.236 |
0.0564 |
|
Mercury |
0.138 |
0.0330 |
|
Gold |
0.130 |
0.0310 |
|
Lead |
0.128 |
0.0305 |
Values
are at Room Temperature and Atmospheric Pressure unless otherwise
stated.
SPECIFIC HEAT HOMEWORK PROBLEMS:
1) When a 50.0 gram piece of nickel absorbs 350.0 J of heat, the
temperature of the nickel changes from 20.0 0C to 36.0 0C.
What is the specific heat of nickel?
2) A solar-heating specialist is considering paraffin as a possible
solar-heat collector. How many kilograms of paraffin would be needed to
collect as much energy as 4.78 x 103 kg of water? The
specific heat of paraffin is 2.9 J / g 0C. (Hint: Assume the
same temperature change.)
3) Calculate the quantity of heat that must be removed from 200.0
grams of ethyl alcohol, C2H6O to cool it from 25.0
0C to 10.0 0C. (ethyl alcohol = 2.45 J / g 0C)
4) How much energy is required to heat a #10 iron nail with a mass of
7.0 grams from 25.0 0C until it becomes red hot at 750 0C?
5) If 5750 J of energy are added to a 455 gram piece of granite at
24.0 0C, what is the final temperature of the granite?
6) A 30.0 gram sample of an unknown metal is heated from 22.0 0C
to 59.2 0C. During the process, 1.00 kJ of energy is absorbed
by the metal. What is the specific heat of the metal?
SPECIFIC HEAT PRACTICE ANSWERS:
1) 0.438 J / g 0C
2) 6.9 x 103 kg paraffin
3) 7350 J or 7.35 kJ
4) 2.3 kJ
5) 39.7 0C
6) 0.896 J / g 0C
E-mail the Answers or bring it to the next class.
|
